Hình chóp đều là hình chóp có mặt đáy là tam giác đều hoặc tứ giác đều. Trong đó, với mặt là tam giác đều thì ta gọi là hình chóp tam giác đều. Nếu hình chóp có đáy là hình vuông thì ta gọi đó là hình chóp tứ giác đều.
Hình chóp đều là một phần kiến thức quan trọng trong môn Toán hình học lớp 8. Để giúp các bạn học sinh dễ dàng nẵm vững kiến thức này. Sau đây ITQNU xin được chia sẻ đến bạn các kiến thức về hình chóp đều.
Định nghĩa hình chóp đều
Trước hết để bắt đầu bài học cũng như giúp các bạn ôn lại kiến thức cũng như định nghĩa về hình chóp đều. Qua đó giúp các bạn nhớ lại và tổng hợp lại kiến thức một cách chi tiết nhất. Thì ngay sau đây sẽ là khái niệm – định nghĩa về hình chóp đều.
Ở một hình chóp nếu các mặt bên là tam giác cân với các cạnh bên bằng nhau (nhưng chưa chắc là tam giác đều). Ngoài ra có đáy là hình đa giác đều thì ta gọi đây được gọi là hình chóp đều. Nói ngắn gọi, để hình chóp là một hình chóp đều cần phải thỏa mãn hai tính chất sau:
- Có đáy là các đa giác đều (hình vuông, hình tam giác đều,..)
- Tâm của đáy trùng với chân đường cao của hình chóp
Thể tích của hình chóp đều được tính bằng công thức: V = ⅓ S.h
Chú ý rằng:
- Trong tam giác đều, tâm đều là giao điểm 3 đường trung tuyến trong tam giác. Cũng là đường cao, trung trực, phân giác trong.
- Trong hình vuông, tâm là giao điểm của hai đường chéo.
- Hình chóp tam giác đều là hình chóp đều với đáy là tam giác đều và mặt bên là tam giác cân (chưa đều).
- Hình chóp tứ giác đều là hình chóp đều có đáy là tứ giác đều. Cụ thể là hình vuông với các mặt bên là tam giác cân.
Ta có thể liên hệ giữa hình chóp đều và tứ diện đều như sau:
- Hình chóp tam giác đều có cạnh bên không chắc chắn bằng đáy thì chóp của tam giác có thêm điều kiện. Đó là cạnh bên bằng đáy và là một tứ diện đều.
- Hình tứ diện đều là hình chóp tác giác đều đặt biệt mà ở đó có thêm cạnh bên bằng chiều dài cạnh đáy.
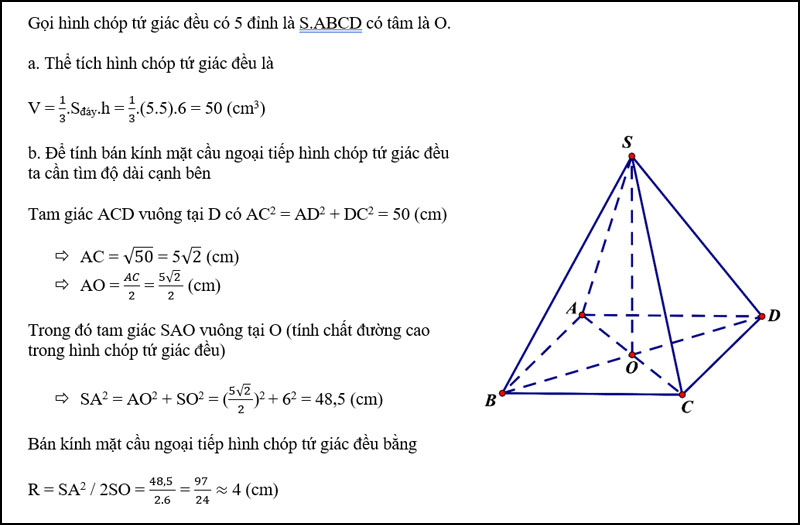
Hướng dẫn các bước vẽ hình chóp đều
Tùy vào dạng bài và yêu cầu của đề bài mà chúng ta sẽ vẽ hình chóp tam giác đều hoặc hình chóp tứ giác đều. Dưới đây là hướng dẫn các bước vẽ hình chóp đều.
Cách vẽ hình chóp tam giác đều
Dưới đây là các bước để các bạn có thể vẽ hình chóp tam giác đều nhanh chóng và dễ dàng nhất:
- Bước 1: Vẽ đáy là hình tam giác đều
- Bước 2: Vẽ các cạnh bên sao cho bằng nhau
- Bước 3: Vẽ các mặt bên với các tam giác cân bằng nhau
- Bước 4: Chân đường cao sẽ trùng với chân của đáy
- Bước 5: Góc tạo bởi cạnh bên (mặt đáy) và mặt đáy bằng nhau
Cách vẽ hình chóp tứ giác đề
Dưới đây là cách vẽ hình chóp tứ giác đều chi tiết nhất qua các bước sau:
- Bước 1: Vẽ đáy là hình vuông
- Bước 2: Vẽ các cạnh bên bằng nhau
- Bước 3: Vẽ các mặt bên là các tam giác cân bằng nhau
- Bước 4: Chân đường cao trùng với tâm của mặt phẳng đáy
- Bước 5: Góc tạo bởi cạnh bên (mặt đáy) và mặt đáy bằng nhau
Các công thức hình chóp đều
Và đối với mỗi hình học thì chúng ta đều có công thức tính diện tích và thể tích của nó. Và hình chóp đều cũng vậy, sau đây là công thức tính diện tích hình chóp đều. Cũng như công thức tính thể tích hình chóp đều. Các bạn có thể tham khảo lại ngay sau đây:
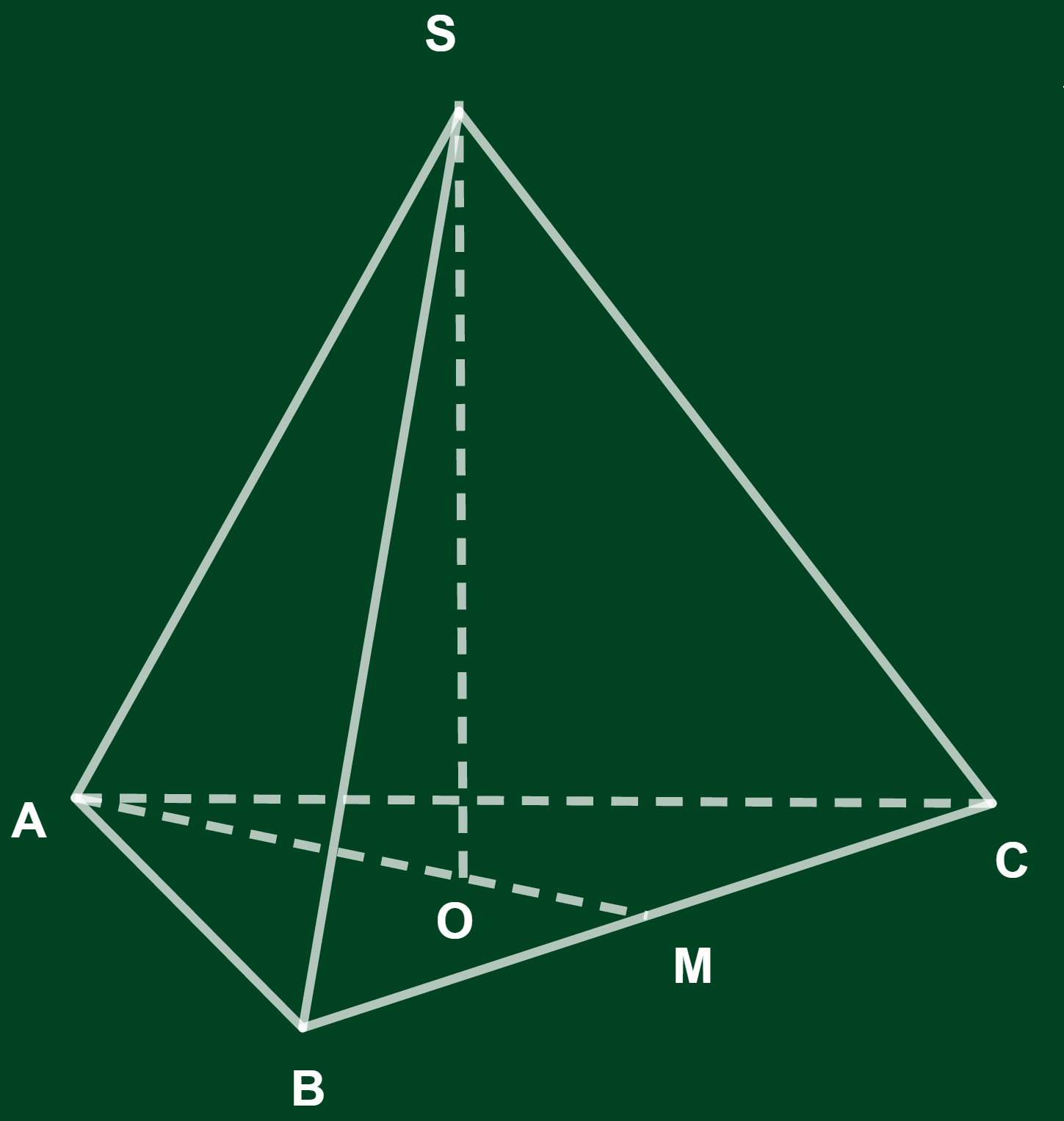
Công thức tính diện tích của hình chóp đều
Diện tích xung quanh của hình chóp đều sẽ bằng tích của nửa chu vi đáy với trung đoạn:
Sxq = p.d
(với p là nửa chu vi đáy, d là trung đoạn)
Diện tích toàn phần của hình chóp sẽ bằng tổng của diện tích xung quanh và diện tích mặt đáy. Ta có công thức sau đây:
Stp = Sxq + S
(với S là diện tích đáy)
Công thức tính thể tích của hình chóp đều
Thể tích của hình chóp bằng một phần ba của diện tích đáy nhân với chiều cao:
V = 1/3S.h
(với S là diện tích đáy và h là chiều cao)
Ví dụ về tính thể tích và diện tích hình chóp đều
Bài 1: Cho một hình chóp tứ giác đều S.ABCD với đáy ABCD là hình vuông, cạnh đáy có chiều dài là 8cm và chiều cao là 10cm. Yêu cầu: hãy tính diện tích xung quanh và diện tích toàn phần của hình chóp. Sau đó tính thể tích của khối chóp.
Lời giải:
Đầu tiên ta có ACBC là hình vuông, nửa chu vi của hình vuông sẽ bằng:
p= 8 + 8 + 8 + 8/ 2 = 16 (cm)
BD = AC = √ (82 + 82) = 8√ 2 ( cm ) ⇒ AO = BO = CO = DO = 4√ 2 ( cm )
Do đó:
- Diện tích xung quanh của hình chóp đều là Sxq = p.d = p.OB = 16.4√ 2 = 64√ 2 ( cm2 )
- Diện tích toàn phần của hình chóp đều là: Stp = Sxq + SABCD = 64√ 2 + 82 = 64 + 64√ 2 ( cm2 )
- Thể tích của hình chóp đều là V = 1/3S.h = 1/3.SABCD.SO = 1/3.82.10 = 640/3( cm3 )
Các dạng toán thường gặp với hình chóp đều
Thông thường đối với hình chóp đều chúng ta cũng sẽ có những dạng toán thường gặp. Và để giúp các bạn tiếp cận các dạng toán đa dạng. Cũng như biết cách để giải các dạng toán này. Thì ngay sau đây là các dạng toán thường gặp đối với hình chóp đều.
Dạng 1
Xác định mối quan hệ giữa các yếu tố của hình chóp như cạnh, mặt phẳng… trong hình chóp đều và hình chóp cụt đều.
Phương pháp giải:
- Ta sử dụng mối quan hệ song song và vuông góc của các đường thẳng, các mặt phẳng, các đường thẳng và mặt phẳng với nhau
- Ta sử dụng kiến thức về hình chóp đều
Dạng 2
Xác định độ dài của cạnh, diện tích xung quanh, diện tích toàn phần và thể tích của hình chóp đều hoặc hình chóp cụt đều.
Phương pháp giải:
Sử dụng công thức như sau: Sxq = p.d (với p là nửa chu vi đáy, d là trung đoạn)
- Diện tích toàn phần sẽ bằng tổng của diện tích xung quanh và diện tích đáy
- Đối với hình chóp, để xác định được diện tích xung quanh thì ta tính tổng diện tích của các mặt bên
- Để tính diện tích xung quanh một hình chóp cụt đều, hãy tính diện tích một mặt bên và nhân nó với số mặt bên hoặc trừ diện tích xung quanh hình chóp nhỏ với diện tích xung quanh hình chóp.
- Thể tích của hình chóp bằng một phần ba của diện tích đáy nhân với chiều cao: V = 1/3S.h
Như vậy, ITQNU.VN vừa chia sẻ đến bạn các kiến thức cơ bản liên quan đến hình chóp đều. Có thể thấy, kiến thức về hình chóp là kiến thức trọng tâm và quan trọng trong bộ môn toán hình học lớp 8. Hy vọng qua bài viết này, các bạn học có thể nắm vững hơn các kiến thức cơ bản về hình chóp đều.