TAM GIÁC ĐỀU: Định nghĩa, tính chất, công thức và dấu hiệu nhận biết

Tiếp theo trong chuyên mục Hình học thì ngay sau đây. Chúng ta sẽ cùng nhau ôn lại định nghĩa, tính chất cũng như các dấu hiệu nhận biết về tam giác đều.

Có thể nói tam giác đều là một trong những dạng hình học mà chúng ta gặp khá nhiều và phổ biến trong các bài tập, bài toán hình. Do đó, chúng ta cần phải nắm vững các kiến thức về tam giác đều. Để có thể giải bài tập cũng như hoàn thành tốt các bài kiểm tra đạt kết quả cao nhất.

Và ngay sau đây xin mời các em cùng ôn lại các kiến thức về tam giác đều dưới đây.

Định nghĩa về tam giác đều

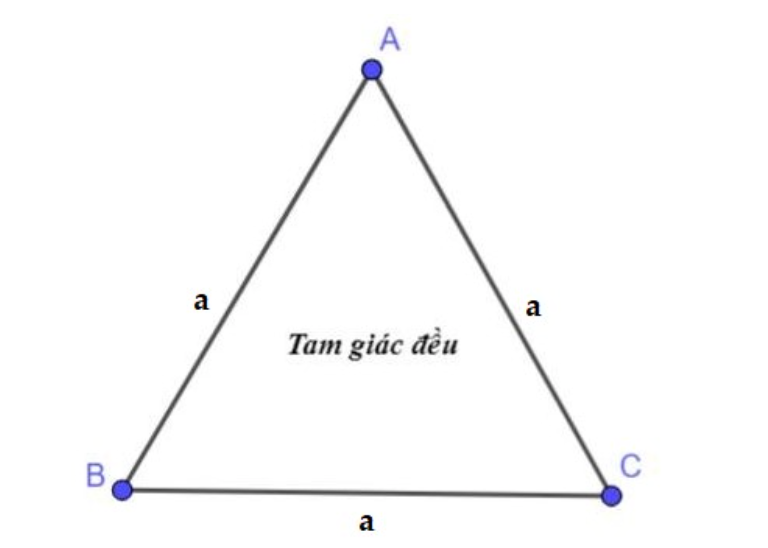
Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau hoặc tương đương ba góc bằng nhau và bằng 60°. Nó là một đa giác đều với số cạnh bằng 3.

Trong tam giác ABC đều có AB = AC = BC.

Hệ quả:

• Trong một tam giác đều thì mỗi góc bằng 60°
• Nếu một tam giác có 3 góc bằng nhau thì đó là tam giác đều.
• Nếu một tam giác cân có 1 góc bằng 60° thì đó là tam giác đều.

Tính chất của tam giác đều

Trong tam giác đều gồm có 5 tính chất, đó là:

1. Trong một tam giác đều, mỗi góc bằng 60⁰. (Tam giác ABC đều  ∠A = ∠B = ∠C = 60⁰.)
2. Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều. ( ∠A = ∠B = ∠C thì là tam giác ABC đều.)
3. Nếu một tam giác cân có một góc bằng 60⁰ thì tam giác đó là tam giác đều.
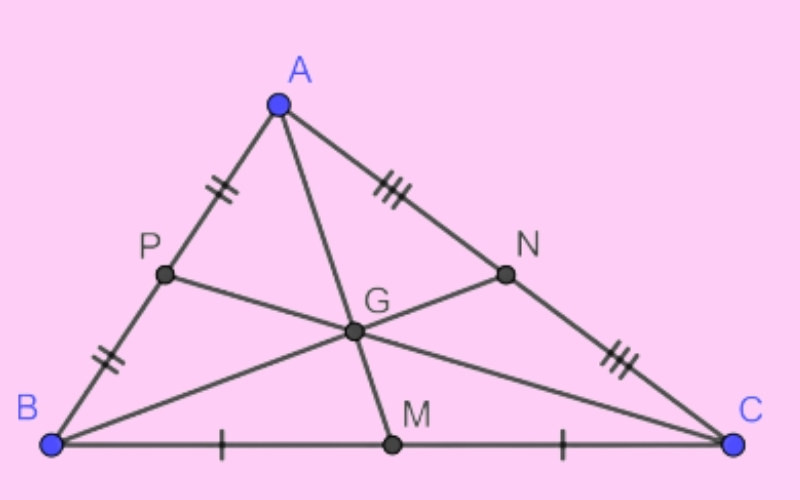
4. Trong tam giác đều, đường trung tuyến của tam giác đồng thời là đường cao và đường phân giác của tam giác đó.
5. Tam giác ABC đều có AD là đường trung tuyến kẻ từ đỉnh A. Khi đó, AD là đường cao và đường phân giác của tam giác ABC.

Đây là những tính chất vô cùng quan trong để các em có thể áp dụng vào bài tập. Vì vậy các em hãy ghi nhớ thật kỹ 5 tính chất của tam giác đều trên đây. Để có thể áp dụng giải bài tập một cách tốt nhất.

Dấu hiệu nhận biết của tam giác đều

Nếu trong tam giác đều có 5 tính chất thì dấu hiệu của tam giác đều chỉ có 4 dấu hiệu như sau:

1. Tam giác có 3 cạnh bằng nhau là tam giác đều.
2. Tam giác có 3 góc bằng nhau là tam giác đều.
3. Tam giác cân có một góc bằng 60° là tam giác đều.
4. Tam giác có 2 góc bằng 60 độ là tam giác đều.

Các công thức trong tam giác đều

Tam giác đều có tất cả 5 công thức, bao gồm các công thức sau:

1. Công thức tính diện tích của tam giác đều

2. Công thức tính chu vi của tam giác đều

P = 3a

3. Công thức tính bán kính đường tròn ngoại tiếp trong tam giác đều

4. Công thức tính bán kính đường tròn nội tiếp trong tam giác đều

Chú ý: Trọng tâm của tam giác cũng là tâm của đường tròn ngoại tiếp và đường tròn nội tiếp.

5. Công thức tính đường cao trong tam giác đều

Trong đó: a là độ dài cạnh của tam giác đều.

Đây là những công thức rất quan trọng để các em có thể áp dụng vào bài tập.

Ứng dụng của tam giác đều trong đời sống

Tam giác đều là 1 hình dạng phổ biến đối với mỗi con người. Và nó được dùng làm đồ chơi cho trẻ em có dạng hình tam giác đều. Hay còn được tạo ra thành những mô hình làm bằng nhựa để cho các em học sinh có thể học tập và nhận biết….

Vậy là chúng ta đã cùng nhau ôn lại những kiến thức vô cùng bổ ích của tam giác đều và sau đây chúng ta cùng luyện tập để có thể hiểu hơn và nhớ bài hơn.

Các bài tập về tam giác đều

Và để giúp các em có thể ghi nhớ một cách tốt nhất các kiến thức về tam giác đều. Cũng như áp dụng và vận dụng các kiến thức về tính chất, dấu hiệu, công thức tam giác đều hiệu quả. Thì ngay sau đây sẽ là một số bài tập vận dụng:

Bài tập 1: Cho tam giác đều ABC có AB bằng 3 (cm). Hãy tính đường cao và diện tích của tam giác đều?

Lời giải:

Đáp số:……..

Bài tập 2: Cho tam giác ABC đều có AB = 5 (cm). Hỏi chu vi tam giác đều bằng bao nhiêu?

Lời giải:

Chu vi tam giác đều là:

Áp dụng công thức: P = 3a

=> P = 3.5 = 15 (cm).

Đáp số:………

Tổng kết

Như vậy trên đây chúng ta đã cùng nhau ôn lại các kiến thức về tam giác đều. Bao gồm định nghĩa, các tính chất, dấu hiệu nhận biết và công thức của tam giác đều rồi.

Hi vọng với những kiến thức bổ ích này sẽ giúp các em có thể ôn tập và rèn luyện lại kiến thức về tam giác đều của mình một cách tốt nhất.