Tích có hướng tích vô hướng của hai Vector được định nghĩa như thế nào? Cũng như tính ứng dụng và các tính chất của tích vô hướng và tích có hướng ra sao. Thì ngay sau đây xin mời các bạn chúng ta hãy cùng nhau ôn tập lại nhé.
Giới thiệu về Vector
Trong toán học và vật lý, vector là đại lượng có hướng và độ lớn, được biểu diễn dưới dạng một mũi tên trong không gian. Vector đóng vai trò quan trọng trong nhiều lĩnh vực như hình học, cơ học, đồ họa máy tính và khoa học máy tính. Hai phép toán quan trọng liên quan đến vector là tích vô hướng (dot product) và tích có hướng (cross product).
Tích có hướng tích vô hướng của hai vector
Trong đại số vector, có hai phép nhân quan trọng giữa hai vector là tích vô hướng (dot product) và tích có hướng (cross product). Mỗi phép toán này có ý nghĩa và ứng dụng khác nhau trong toán học, vật lý và kỹ thuật.
Tích vô hướng (Dot Product)
Tích vô hướng của hai vector là một phép nhân tạo ra một số vô hướng (scalar). Công thức của tích vô hướng giữa hai vector A và B được tính như sau:
A⋅B=∣A∣∣B∣cosθA \cdot B = |A| |B| \cos\thetaA⋅B=∣A∣∣B∣cosθ
Trong đó:
- AAA và BBB là hai vector,
- ∣A∣|A|∣A∣ và ∣B∣|B|∣B∣ là độ dài (độ lớn) của hai vector,
- θ\thetaθ là góc giữa hai vector.
Biểu diễn tọa độ:
Nếu hai vector được biểu diễn dưới dạng tọa độ trong không gian 2D hoặc 3D: A=(a1,a2,a3),B=(b1,b2,b3)A = (a_1, a_2, a_3), \quad B = (b_1, b_2, b_3)A=(a1,a2,a3),B=(b1,b2,b3)
Thì tích vô hướng có thể tính như sau: A⋅B=a1b1+a2b2+a3b3A \cdot B = a_1b_1 + a_2b_2 + a_3b_3A⋅B=a1b1+a2b2+a3b3
Ứng dụng của tích vô hướng
- Tính góc giữa hai vector: Sử dụng công thức: cosθ=A⋅B∣A∣∣B∣\cos\theta = \frac{A \cdot B}{|A| |B|}cosθ=∣A∣∣B∣A⋅B
- Xác định hai vector có vuông góc hay không: Nếu A⋅B=0A \cdot B = 0A⋅B=0, thì hai vector vuông góc với nhau.
- Ứng dụng trong đồ họa máy tính, xác định độ chiếu sáng trong mô hình ánh sáng.

Tích có hướng (Cross Product)
Tích có hướng của hai vector tạo ra một vector mới vuông góc với cả hai vector ban đầu. Công thức tổng quát của tích có hướng là:
A×B=∣A∣∣B∣sinθ n^A \times B = |A| |B| \sin\theta \ \hat{n}A×B=∣A∣∣B∣sinθ n^
Trong đó:
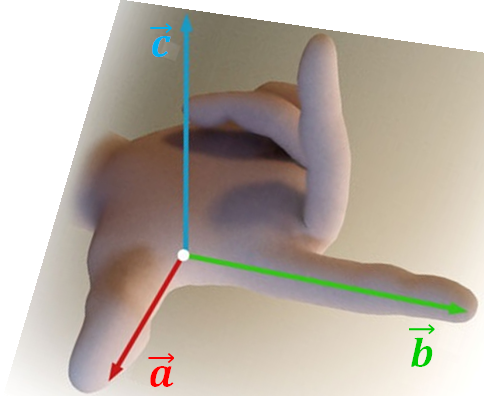
- n^\hat{n}n^ là vector đơn vị vuông góc với cả AAA và BBB theo quy tắc bàn tay phải,
- θ\thetaθ là góc giữa hai vector.
Biểu diễn tọa độ:
Nếu hai vector được cho trong không gian 3D: A=(a1,a2,a3),B=(b1,b2,b3)A = (a_1, a_2, a_3), \quad B = (b_1, b_2, b_3)A=(a1,a2,a3),B=(b1,b2,b3)
Thì tích có hướng được tính theo định thức: A×B=∣i^j^k^a1a2a3b1b2b3∣A \times B = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}A×B=i^a1b1j^a2b2k^a3b3
Tính ra: A×B=[a2b3−a3b2a3b1−a1b3a1b2−a2b1]A \times B = \begin{bmatrix} a_2b_3 – a_3b_2 \\ a_3b_1 – a_1b_3 \\ a_1b_2 – a_2b_1 \end{bmatrix}A×B=a2b3−a3b2a3b1−a1b3a1b2−a2b1
Tính chất của tích có hướng:
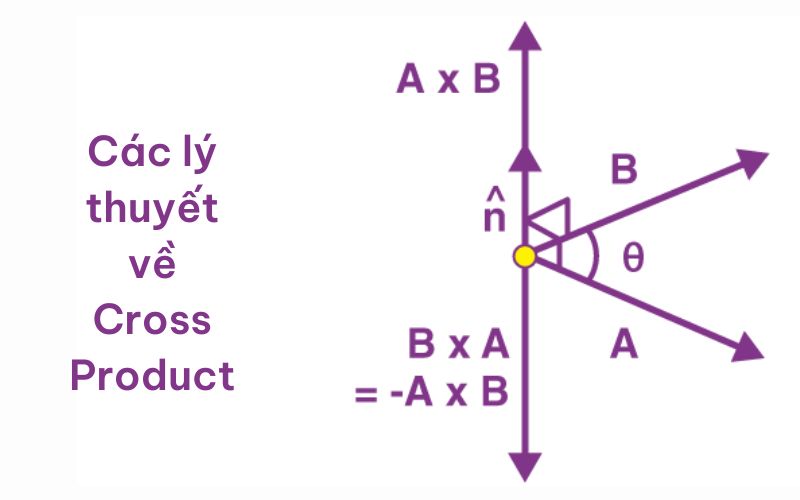
- Vuông góc với hai vector ban đầu: A×BA \times BA×B luôn vuông góc với cả AAA và BBB.
- Không giao hoán: A×B=−(B×A)A \times B = – (B \times A)A×B=−(B×A).
- Nếu hai vector song song, tích có hướng bằng 0.
Ứng dụng của tích có hướng:
- Tính diện tích tam giác: Diện tích tam giác tạo bởi hai vector AAA và BBB là: S=12∣A×B∣S = \frac{1}{2} |A \times B|S=21∣A×B∣
- Tính mô-men lực trong vật lý.
- Ứng dụng trong đồ họa máy tính, đặc biệt là tính toán pháp tuyến trong mô hình 3D.
So sánh Tích vô hướng và Tích có hướng
| Đặc điểm | Tích Vô Hướng A⋅BA \cdot BA⋅B | Tích Có Hướng A×BA \times BA×B |
|---|---|---|
| Kết quả | Một số vô hướng (scalar) | Một vector |
| Công thức | ( A \cdot B = | A |
| Ý nghĩa hình học | Độ lớn liên quan đến độ dài và góc giữa hai vector | Một vector vuông góc với hai vector ban đầu |
| Ứng dụng | Tính góc, kiểm tra vuông góc, mô hình ánh sáng | Xác định mặt phẳng, tính diện tích, vật lý, đồ họa 3D |
Tích vô hướng và tích có hướng là hai phép toán quan trọng trong đại số vector. Tích vô hướng dùng để đo độ lớn liên quan giữa hai vector, trong khi tích có hướng tạo ra một vector vuông góc với hai vector ban đầu. Cả hai phép toán đều có ứng dụng quan trọng trong vật lý, đồ họa máy tính, kỹ thuật và nhiều lĩnh vực khác.
Như vậy trên đây chúng tôi đã chia sẻ cũng như cùng nhau với các bạn ôn tập lại kiến thức về tích có hướng tích vô hướng của hai vectơ. Cũng như các tính chất và ứng dụng của 2 kiến thức này. Hi vọng với những kiến thức về toán học này sẽ giúp các bạn ôn tập cũng như nắm vứng kiến thức để áp dụng vào giải các bài toán một cách tốt nhất.